Rでカイ２乗検定

R言語を使いWeb教材「ハンバーガーショップで学ぶ楽しい統計学」¹の「カイ２乗検定」について進めていきます（第3回）。

ワクワクとモグモグの、ポテトとチキンの1日の売り上げ個数を調べ、その個数は次の表（クロス集計表）にする。

帰無仮説H₀:チキンとポテトの売り上げの割合に関して、モグモグとワクワクの間に差はない。→2つの変数は独立（連関がない）である。

対立仮説H₁: チキンとポテトの売り上げの割合に関して、モグモグとワクワクの間に差はある。→2つの変数は独立（連関がある）ではない。

先ほどの観測度数を記したクロス集計表に周辺度数と総度数を加えて記すと以下のようになる。

（行の計および列の計を周辺度数といい、特に行と列の計が交わる値=1,000を総度数という）。

期待度数は差がないという帰無仮説のもとで、どのくらいの度数をとるのか期待される度数をいうので、「（セルが属する行の周辺度数×セルが属する列の周辺度数）÷総度数」で求まる。

カイ二乗値は「 （（（観測度数－期待度数）の２乗）÷期待度数）の総和」で求まる。

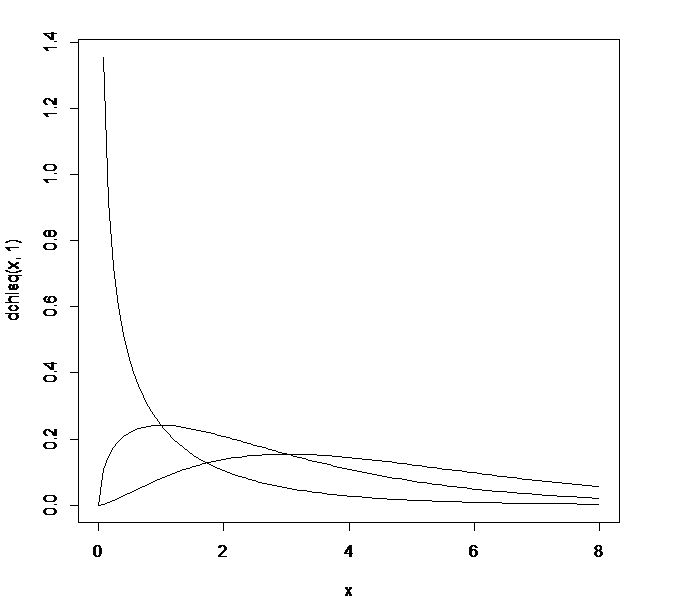
自由度を変化させた(df=1→3→5)ときのカイ二乗分布の変化を示す（正規分布やt分布のように0を中心にした左右対称の分布にはならないが、自由度が大きくなると左右対称の形に近づく）。

カイ２乗検定

自由度（df: degrees of freedom）は、一般的には行と列がある二次元の表の場合の自由度は「（行の数－1）×（列の数－1）」と示される。 つまりポテト・チキンまたは、ワクワク・モグモグの 1つの値が決まれば、残りは自動的にきまるので(2-1)* (2-1)=1となる。

有意水準5%と1%を求める。

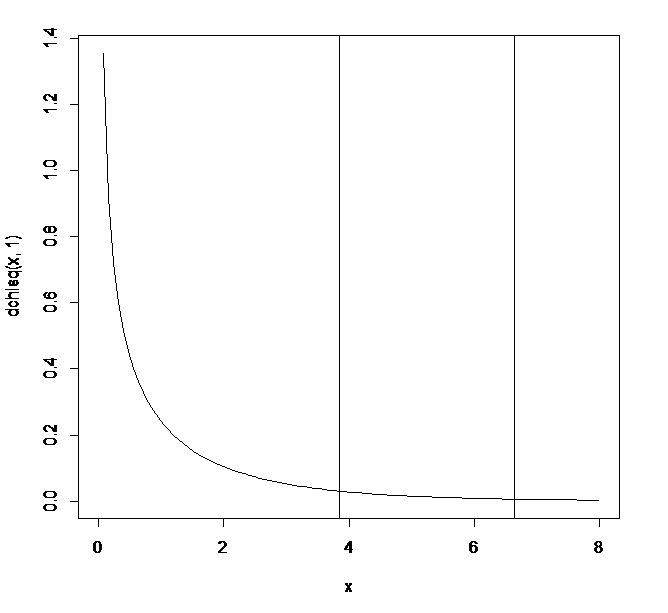
自由度1で有意水準5%と1%を図示すると以下のようになる。

今回は「有意水準として5%をとるとする」とあるので、棄却域はカイ二乗(= 4.464286)より5%の場合の棄却域に入るため、帰無仮説は棄却され、対立仮説を採択します。つまり、「 ワクワクとモグモグではポテトとチキン売り上げの割合に差がある」といいう結論になります。

カイ二乗検定を関数chisq.test()で一発検定し、correct=FALSEはデフォルトで実行される連続性の補正を行わない。

p値（p-value）は、帰無仮説が正しいという仮定のもので計算した値（今回はカイ二乗）について、それ以上で得られる確率のこと。

カイ二乗のp値の計算は以下のように行う（なおカイ二乗値の後には自由度を入れ、上側確率の場合は更にその後にcorrect=FALSEを加える）。

有意水準5%(0.05)の値より小さいのでp値からも帰無仮説が棄却されることがわかります。