R言語を使いWeb教材「ハンバーガーショップで学ぶ楽しい統計学」1の「分散分析(2要因)」について進めていきます(第7回)。
2つの要因では?
要因と水準
2つある要因と、それぞれの要因について2つの水準を示すと以下のようになる。
- 食感について
要因 | 水準1 | 水準2 |
食感 | クリスピー | 普通の衣 |
- 味付けについて
要因 | 水準1 | 水準2 |
味付け | 辛口 | 普通味 |
つまり「 クリスピーで辛口」、「クリスピーで普通味」、「普通の衣で辛口」、「普通の衣で普通味」 4種類のチキンが考えられることになる。
データを集める
4種類のチキンをそれぞれ15個ずつ60人に食べてもらい、そのおいしさについて100点満点で点数をつけてもらう。
その場合のデータは次のようになる。
>
クリスピーで辛口<-c(65,85,75,85,75,80,90,75,85,65,75,85,80,85,90)
> クリスピーで普通味<-c(65,70,80,75,70,60,65,70,85,60,65,75,70,80,75)
> 普通の衣で辛口<-c(70,65,85,80,75,65,75,60,85,65,75,70,65,80,75)
> 普通の衣で普通味<-c(70,70,85,80,65,75,65,85,80,60,70,75,70,80,85)
> 味<-c(クリスピーで辛口,クリスピーで普通味,普通の衣で辛口,普通の衣で普通味)
> 味
[1] 65 85 75 85 75 80 90 75 85 65 75 85 80 85 90 65 70 80 75 70 60 65 70 85
[25] 60 65 75 70 80 75 70 65 85 80 75 65 75 60 85 65 75 70 65 80 75 70 70 85
[49] 80 65 75 65 85 80 60 70 75 70 80 85
> 全データ<-cbind(クリスピーで辛口,クリスピーで普通味,普通の衣で辛口,普通の衣で普通味)
> 全データ
クリスピーで辛口 クリスピーで普通味 普通の衣で辛口 普通の衣で普通味
[1,] 65 65 70 70
[2,] 85 70 65 70
[3,] 75 80 85 85
[4,] 85 75 80 80
[5,] 75 70 75 65
[6,] 80 60 65 75
[7,] 90 65 75 65
[8,] 75 70 60 85
[9,] 85 85 85 80
[10,] 65 60 65 60
[11,] 75 65 75 70
[12,] 85 75 70 75
[13,] 80 70 65 70
[14,] 85 80 80 80
[15,] 90 75 75 85
それぞれの平均を求める。
> 水準平均<-colMeans(全データ)
> 水準平均
クリスピーで辛口 クリスピーで普通味 普通の衣で辛口 普通の衣で普通味
79.66667 71.00000 72.66667 74.33333
次に標準偏差も求める。
> クリスピーで辛口の標準偏差<-sqrt(mean((クリスピーで辛口-mean(クリスピーで辛口))^2))
> クリスピーで辛口の標準偏差
[1] 7.630349
> クリスピーで普通味の標準偏差<-sqrt(mean((クリスピーで普通味-mean(クリスピーで普通味))^2))
> クリスピーで普通味の標準偏差
[1] 7.118052
> 普通の衣で辛口の標準偏差<-sqrt(mean((普通の衣で辛口-mean(普通の衣で辛口))^2))
> 普通の衣で辛口の標準偏差
[1] 7.498148
> 普通の衣で普通味の標準偏差<-sqrt(mean((普通の衣で普通味-mean(普通の衣で普通味))^2))
> 普通の衣で普通味の標準偏差
[1] 7.717225
ズレの分解
全体の平均からのズレは、食感の要因によるズレ(主効果)+味付けの要因によるズレあ(主効果)+食感の要因と味付けの要因の組み合わせによるズレ(交互作用効果)+残差となる。
2要因の分散分析
2要因分散分析の帰無仮説は、残差に対して、「食感の要因によるズレ」が大きければ、この主効果が大きく、残差に対して、「味付けの要因によるズレ」が大きければ、この主効果が大きい。また、残差に対して、交互作用によるズレが大きければ、交互作用が大きいことがわかる。
帰無仮説H0: 食感の要因による差がなく、味付けの要因による差がなく、また交互作用による差もない。
対立仮説H1: 食感の要因による差があるか、味付けの要因による差があるか、または、交互作用による差があるか、どれか1つが成り立つ。
具体的には、次の7つの場合が考えられる。
- 食感の要因の主効果だけが有意
- 味付けの要因の主効果だけが有意
- 交互作用だけが有意
- 食感の要因の主効果と味付けの要因の主効果が有意
- 食感の要因の主効果と交互作用が有意
- 味付けの要因の主効果と交互作用が有意
- 食感の要因の主効果と味付けの要因の主効果と交互作用のすべてが有意
2要因の分散分析表
食感の要因によるズレを計算する
- 前処理
> 全体平均行列2列<-matrix(rep(mean(味),30),nrow=15,ncol=2)
> 全体平均行列2列
[,1] [,2]
[1,] 74.41667 74.41667
[2,] 74.41667 74.41667
[3,] 74.41667 74.41667
[4,] 74.41667 74.41667
[5,] 74.41667 74.41667
[6,] 74.41667 74.41667
[7,] 74.41667 74.41667
[8,] 74.41667 74.41667
[9,] 74.41667 74.41667
[10,] 74.41667 74.41667
[11,] 74.41667 74.41667
[12,] 74.41667 74.41667
[13,] 74.41667 74.41667
[14,] 74.41667 74.41667
[15,] 74.41667 74.41667
- 食感のうちクリスピー
> クリスピー<-全データ[,c(1,2)]
> クリスピー平均行列<-matrix(rep(mean(クリスピー),30),nrow=15,ncol=2)
> クリスピー平均行列
[,1] [,2]
[1,] 75.33333 75.33333
[2,] 75.33333 75.33333
[3,] 75.33333 75.33333
[4,] 75.33333 75.33333
[5,] 75.33333 75.33333
[6,] 75.33333 75.33333
[7,] 75.33333 75.33333
[8,] 75.33333 75.33333
[9,] 75.33333 75.33333
[10,] 75.33333 75.33333
[11,] 75.33333 75.33333
[12,] 75.33333 75.33333
[13,] 75.33333 75.33333
[14,] 75.33333 75.33333
[15,] 75.33333 75.33333
> クリスピーの水準間平方和<-sum((クリスピー平均行列-全体平均行列2列)^2)
> クリスピーの水準間平方和
[1] 25.20833
- 食感のうち普通の衣
> 普通の衣<-全データ[,c(3,4)]
> 普通の衣平均行列<-matrix(rep(mean(普通の衣),30),nrow=15,ncol=2)
> 普通の衣平均行列
[,1] [,2]
[1,] 73.5 73.5
[2,] 73.5 73.5
[3,] 73.5 73.5
[4,] 73.5 73.5
[5,] 73.5 73.5
[6,] 73.5 73.5
[7,] 73.5 73.5
[8,] 73.5 73.5
[9,] 73.5 73.5
[10,] 73.5 73.5
[11,] 73.5 73.5
[12,] 73.5 73.5
[13,] 73.5 73.5
[14,] 73.5 73.5
[15,] 73.5 73.5
> 普通の衣の水準間平方和<-sum((普通の衣平均行列-全体平均行列2列)^2)
> 普通の衣の水準間平方和
[1] 25.20833
- 食感の要因によるズレ(クリスピーと普通の衣のズレを合計)
> 食感によるズレ<-クリスピーの水準間平方和+普通の衣の水準間平方和
> 食感によるズレ
[1] 50.41667
味付けの要因によるズレを計算する
- 味付けのうち辛口
> 辛口<-全データ[,c(1,3)]
> 辛口平均行列<-matrix(rep(mean(辛口),30),nrow=15,ncol=2)
> 辛口平均行列
[,1] [,2]
[1,] 76.16667 76.16667
[2,] 76.16667 76.16667
[3,] 76.16667 76.16667
[4,] 76.16667 76.16667
[5,] 76.16667 76.16667
[6,] 76.16667 76.16667
[7,] 76.16667 76.16667
[8,] 76.16667 76.16667
[9,] 76.16667 76.16667
[10,] 76.16667 76.16667
[11,] 76.16667 76.16667
[12,] 76.16667 76.16667
[13,] 76.16667 76.16667
[14,] 76.16667 76.16667
[15,] 76.16667 76.16667
> 辛口の水準間平方和<-sum((辛口平均行列-全体平均行列2列)^2)
> 辛口の水準間平方和
[1] 91.875
- 味付けのうち普通
> 普通<-全データ[,c(2,4)]
> 普通平均行列<-matrix(rep(mean(普通),30),nrow=15,ncol=2)
> 普通平均行列
[,1] [,2]
[1,] 72.66667 72.66667
[2,] 72.66667 72.66667
[3,] 72.66667 72.66667
[4,] 72.66667 72.66667
[5,] 72.66667 72.66667
[6,] 72.66667 72.66667
[7,] 72.66667 72.66667
[8,] 72.66667 72.66667
[9,] 72.66667 72.66667
[10,] 72.66667 72.66667
[11,] 72.66667 72.66667
[12,] 72.66667 72.66667
[13,] 72.66667 72.66667
[14,] 72.66667 72.66667
[15,] 72.66667 72.66667
> 普通の水準間平方和<-sum((普通平均行列-全体平均行列2列)^2)
> 普通の水準間平方和
[1] 91.875
- 味付けの要因によるズレ(辛口と普通のズレを合計)
> 味付けによるズレ<-辛口の水準間平方和+普通の水準間平方和
> 味付けによるズレ
[1] 183.75
交互作用によるズレを計算する
相互作用によるズレは、各水準のズレから食感の要因によるズレと味付けの要因によるズレを引いたものである。
> 水準平均平方和<-matrix(rep(水準平均,5),nrow=15,ncol=4,byrow=TRUE)
> 水準平均平方和
[,1] [,2] [,3] [,4]
[1,] 79.66667 71 72.66667 74.33333
[2,] 79.66667 71 72.66667 74.33333
[3,] 79.66667 71 72.66667 74.33333
[4,] 79.66667 71 72.66667 74.33333
[5,] 79.66667 71 72.66667 74.33333
[6,] 79.66667 71 72.66667 74.33333
[7,] 79.66667 71 72.66667 74.33333
[8,] 79.66667 71 72.66667 74.33333
[9,] 79.66667 71 72.66667 74.33333
[10,] 79.66667 71 72.66667 74.33333
[11,] 79.66667 71 72.66667 74.33333
[12,] 79.66667 71 72.66667 74.33333
[13,] 79.66667 71 72.66667 74.33333
[14,] 79.66667 71 72.66667 74.33333
[15,] 79.66667 71 72.66667 74.33333
> 各水準平均の平方和<-sum((水準平均平方和-全体平均行列)^2)
> 各水準平均の平方和
[1] 634.5833
> 交互作用によるズレ<-各水準平均の平方和-食感によるズレ-味付けによるズレ
> 交互作用によるズレ
[1] 400.4167
残差によるズレを計算する
残差は1要因の群内のズレに相当するので、以下のようになる。
> 残差<-sum((全データ-水準平均平方和)^2)
> 残差
[1] 3370
分散分析表をつくる
まずは、全体のズレを計算する。
> 全体のズレ<-食感によるズレ+味付けによるズレ+交互作用によるズレ+残差
> 全体のズレ
[1] 4004.583
次にそれぞれの自由度を計算する。
食感の要因、味付けの要因の自由度は、それぞれの中の条件数から1を引いたものなので(2-1=)1となる。
また、
交互作用の自由度はそれぞれの要因の自由度をかけ算したものになるので、これも(1×1=)1となる。
交互作用の自由度は、それぞれの要因の自由度をかけ算したものなので、これも(1×1=)1となる。
残差の自由度は、全体の自由度から、食感による要因と味付けによる要因、交互作用の自由度を引いたものなので(60-1=)59になる。
次に、平均平方を計算します。平均平方は平方和を自由度でわり算したものです。
最後に、検定統計量Fを計算する。
食感の要因、味付けの要因、交互作用の平均平方をそれぞれ、残差の平均平方で割ったものがFになる。
> 食感のF<-(食感によるズレ/1)/(残差/56)
> 食感のF
[1] 0.8377844
> 味付けのF<-(味付けによるズレ/1)/(残差/56)
> 味付けのF
[1] 3.053412
> 交互作用のF<-(交互作用によるズレ/1)/(残差/56)
> 交互作用のF
[1] 6.653808
今回もRの関数を使い一発で分散分析表をつくることもできる。
- 前処理
> 食感<-factor(c(rep("クリスピー",30),rep("普通の衣",30)))
> 食感
[1] クリスピー クリスピー クリスピー クリスピー クリスピー クリスピー
[7] クリスピー クリスピー クリスピー クリスピー クリスピー クリスピー
[13] クリスピー クリスピー クリスピー クリスピー クリスピー クリスピー
[19] クリスピー クリスピー クリスピー クリスピー クリスピー クリスピー
[25] クリスピー クリスピー クリスピー クリスピー クリスピー クリスピー
[31] 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣
[37] 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣
[43] 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣
[49] 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣
[55] 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣 普通の衣
Levels: クリスピー 普通の衣
> 味付け<-factor(rep(c(rep("辛口",15),rep("普通味",15)),2))
> 味付け
[1] 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口
[11] 辛口 辛口 辛口 辛口 辛口 普通味 普通味 普通味 普通味 普通味
[21] 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味
[31] 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口 辛口
[41] 辛口 辛口 辛口 辛口 辛口 普通味 普通味 普通味 普通味 普通味
[51] 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味 普通味
Levels: 辛口 普通味
- 一般的な分散分析表をつくるためのsummary(aov())関数を実行
> summary(aov(味~食感*味付け))
Df Sum Sq Mean Sq F value Pr(>F)
食感 1 50 50.4 0.838 0.3640
味付け 1 184 183.7 3.053 0.0860 .
食感:味付け 1 400 400.4 6.654 0.0125 *
Residuals 56 3370 60.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
有意差をみる
検定統計量Fの値を見て、それが棄却域にはいるかどうかを判定します。
食感の要因でも味付けの要因でも、残差の自由度が56、要因の自由度が1だったので、以下のようになる。
> qf(0.05,1,56,lower.tail=FALSE)
[1] 4.012973
5%有意水準の場合の棄却域は4.01となるので、食感の要因の検定統計量F(=0.84)、味付けの要因の検定統計量F(=3.05)は、いずれの棄却域にも入らない。したがって、「食感の要因 、味付けによる点数の差はない」という結論になる。しかし、交互作用の検定統計量F(=6.65)は。棄却域には入るので、
主効果に有意差がないので「その要因単独の効果はない」が「交互作用による点数の差はある」ということになる。
交互作用とは
各水準の平均を見てみる。
> 水準平均の表<-matrix(水準平均,nrow=2,ncol=2)
> rownames(水準平均の表)<-c("辛口","普通味")
> colnames(水準平均の表)<-c("クリスピー","普通の衣")
> 水準平均の表
クリスピー 普通の衣
辛口 79.66667 72.66667
普通味 71.00000 74.33333
「クリスピー、辛口は、単独で使うより、両方を使った方がよく、逆に、どちらかを使うくらいなら、普通のチキンの方がよい」ということがわかる。
これを図示して確認してみる。
> interaction.plot(食感,味付け,味)
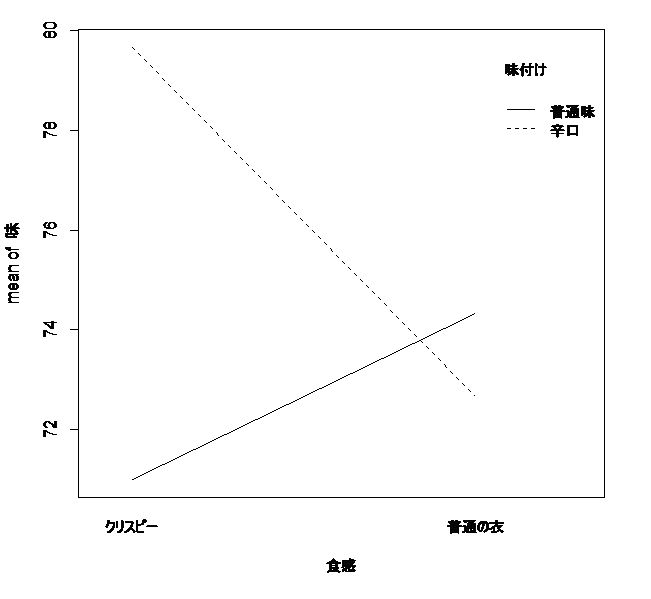
> interaction.plot(味付け,食感,味)
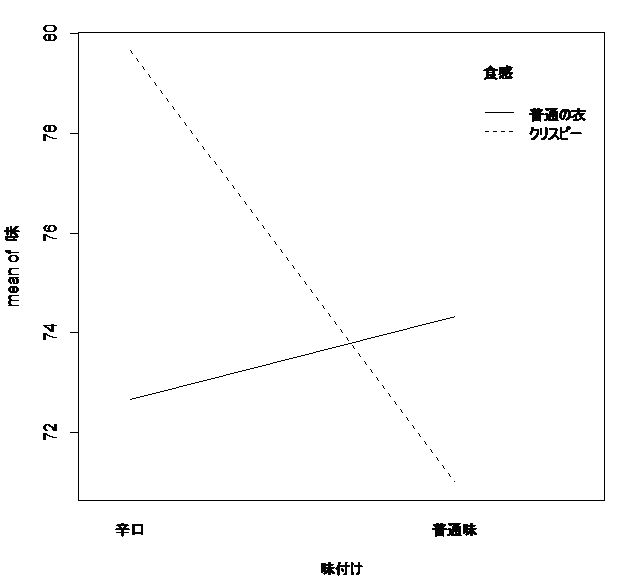
クリスピーか普通の衣かの主効果も、辛口か普通味かの主効果もないけれども、クリスピーのときは辛口がよく、普通の衣のときは普通味のほうがよいという交互作用がでている。つまり、組み合わされる要因によって効果の現れ方が違うということである。
- web教材「ハンバーガーショップで学ぶ楽しい統計学」第7章 分散分析(2要因)http://kogolab.chillout.jp/elearn/hamburger/chap7/sec0.html